[ 알고리즘 기초 ]
#알고리즘 이란?
어떤 문제나 과제를 해결하기 위한 단계적 방법이다.
알고리즘에는 3가지 요소가 있는데 그것은 Sequence, Decision, Repetition 이다.
3가지를 풀이하면,
1) 순서가 있어야 하고
2) 조건에 따른 실행이 가능하고
3) 반복적으로 실행이 가능한 것을 말한다.
1) ~ 3)까지 유한 시간 내 반드시 종료가 돼야 하고 수행의 결과가 존재해야 한다.
부 알고리즘(subAlgorithms)은 복잡한 알고리즘 안에 있는 부분 알고리즘이다.
주 알고리즘과 부 알고리즘의 관계는 Structure Chart로 확인이 가능하다.
이런 용어를 하나씩 인지하고 있으면 언제나 도움이 된다.

알고리즘을 표현하는 방법으로는 UML과 Pseudocode가 있다.
UML은 그림과 도표이고 의사 코드(수도 코드, Pseudocode)는 문자로 표기한다.


#기본적인 알고리즘
덧셈, 뺄셈, 가장 작은 수(미니멈), 가장 큰 수(맥스)가 있고 정렬, 탐색이 존재한다.
정렬은 대표적으로 3개가 있다. 영상이 골 때리지만 뇌리에 정확히 박히게 해 주니 참고하면 좋다.
- Selection Sort : https://www.youtube.com/watch?v=Ns4TPTC8whw
- Bubble Sort : https://www.youtube.com/watch?v=lyZQPjUT5B4
- Insertion Sort : https://www.youtube.com/watch?v=ROalU379l3U
탐색으로는 대표적으로 2개가 있다.
- Sequential : 처음부터 끝까지 순서태로 탐색한다.
- Binary : List의 범위를 1/2씩 분할하여 탐색한다.
#자료형의 크기
자료형이 얼마큼 데이터를 소모하고 있는지 알고 있어야 한다.
요즘 파이썬과 같은 프로그램은 자료형의 크기를 크게 신경 쓰지 않는다.
하지만 C와 같은 프로그래밍 언어를 사용할 때는 매우 중요하게 작용한다.
크기를 계산하지 않고 프로그래밍하면 오류가 발생할 수밖에 없다.
Char형 : 1byte
Int형 : 2 or 4 bytes(대부분 4 bytes)이다.
float형 : 4 bytes
double형 : 8 bytes
#알고리즘 성능 분석
알고리즘의 성능평가를 하기
- 성능 분석 : 복잡도 이론
- 성능 측정 : 실행시간 측정(종료시간 - 시작시간)
- 다른 알고리즘과 비교
복잡도 이론이란
- 공간 복잡도 : 프로그램이 실행되어 작업을 완료하기까지 필요한 메모리 공간
- 시간 복잡도 : 프로그램이 실행되어 작업을 완료하기까지 필요한 시간
# 공간 복잡도와 시간 복잡도
공간 복잡도는 요즘 같은 대용량 시대에 크게 고려 대상은 아니다.
하지만 시간 복잡도는 이야기가 다르다.
시간 복잡도에서 직접적인 영향을 주는 건 단계의 수다.
그래서 이 단계가 얼마나 오래 걸리는 가를 표기하는 방법이 존재한다.
그것이 바로 빅오(BigOh) 표기법이라는 방법이다.
결론부터 이야기하자면 아래 순서대로 오래 걸린다.
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n)
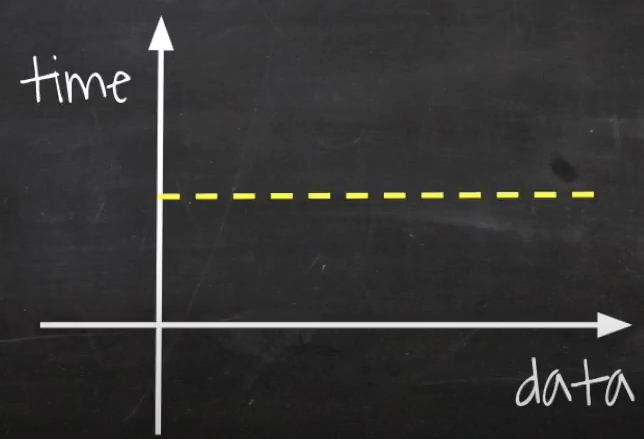
O(1) 은 데이터가 증가함에 따라 성능이 변함이 없다.
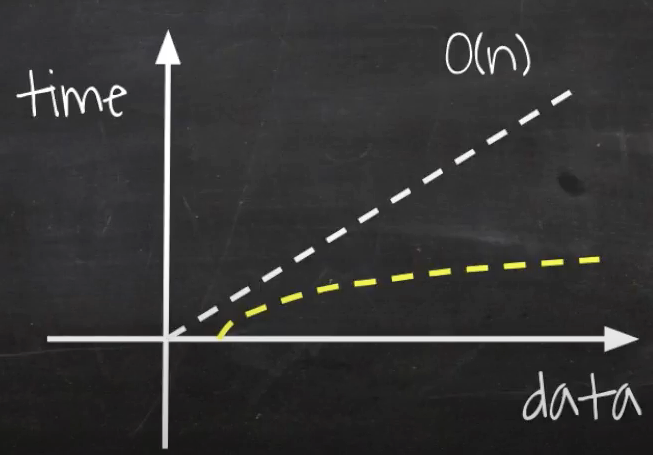
O(n)는 for문이 하나 생긴다.
for문의 i가 데이터가 증가함에 따라 처리 시간도 같이 늘어난다.
def F(n) {
for i in range(len(n)):
print(i)
}
O(n2)는 for문이 두 개가 된다.
for문의 i와 j의 데이터가 클수록 공간과 시간은 더욱 많이 상승한다.
def F(n) {
for i in range(len(n)):
for j in range(len(n)):
print(i + j)
}

O(2n)은 피보나치 수열이다.
1, 1, 2, 3, 5, 8, 13. 21........으로 값이 나온다.
이런 방식의 알고리즘은 시간과 데이터의 양이 급격하게 증가한다.
def F(n, r) {
return F(n-1) + F(n-2) if n >= 2 else n
}
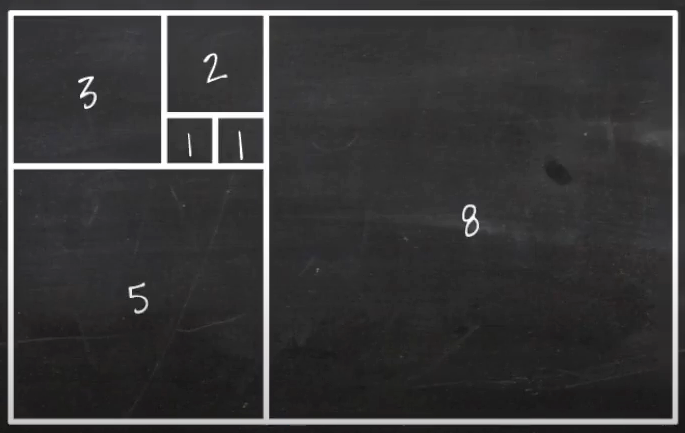

O(log n)은 대표적으로 이진 검색(Binary Search)으로 보면 된다.
여기서 6을 찾을 때 먼저 가운데 값을 확인한다.
가운데 값은 5이고 6과 비교한 후 6보다 값이 작으니까 그 앞 값까지 전부 버린다.
그다음 뒤쪽 데이터인 7과 비교해보면 6보다 크므로 뒤쪽 전부를 버린다.
그럼 6의 자리를 찾게 된다.
이러한 알고리즘은 테이터가 늘어나도 크게 속도에 영향을 주지 않는다.

#빅오(BigOh) 계산법
상수는 제거한다.
O(2n) == O(n) 과 같다.
O(n2 + n2) == O(2n2) == O(n2) 과 같다.
'동굴 속 정보' 카테고리의 다른 글
| 인터뷰에서 중요한 운영체제 질문 1 (0) | 2020.04.29 |
|---|---|
| 인터뷰에서 중요한 알고리즘 질문 2 (0) | 2020.04.27 |
| 최고의 여행용 쌍안경 부쉬넬 레전드 울트라 HD (0) | 2020.04.25 |
| 데이터 전처리의 핵심은 apply 이다. (0) | 2020.04.22 |
| python groupby로 그룹끼리 한줄 정리하기 (1) | 2020.04.20 |



