[ Hash Table ]
해쉬는 중복이 안 되는 것을 목표로 하고 만들어진다. 그래서 어떠한 값이 해쉬로 만들어질 때는 일반적으로 중복이 없다. 다만 기술이 발전하면서 연산 속도가 높아지는 과정을 통해 과거에 안전하다는 해쉬들도 깨지고 있다. MD5가 대표적인 예로 1996년에 collision 문제가 지적되었고 2005년 Birthday Attack으로 안전하지 않은 것이 증명되었다.
다시 원점으로 돌아와서 해쉬는 키값을 통해 중복되지 않는 해쉬를 만들어서 다른 어떤 것들과 함께 있어도 구별이 되어야 한다. 그럼 값들로 이루어진 값을 가지고 있다면 검색에서 엄청나게 빠른 속도를 보여줄 것이다. 이런 기술은 암호화폐로 이어졌고 역시 목표는 중복이 없는 것이다.
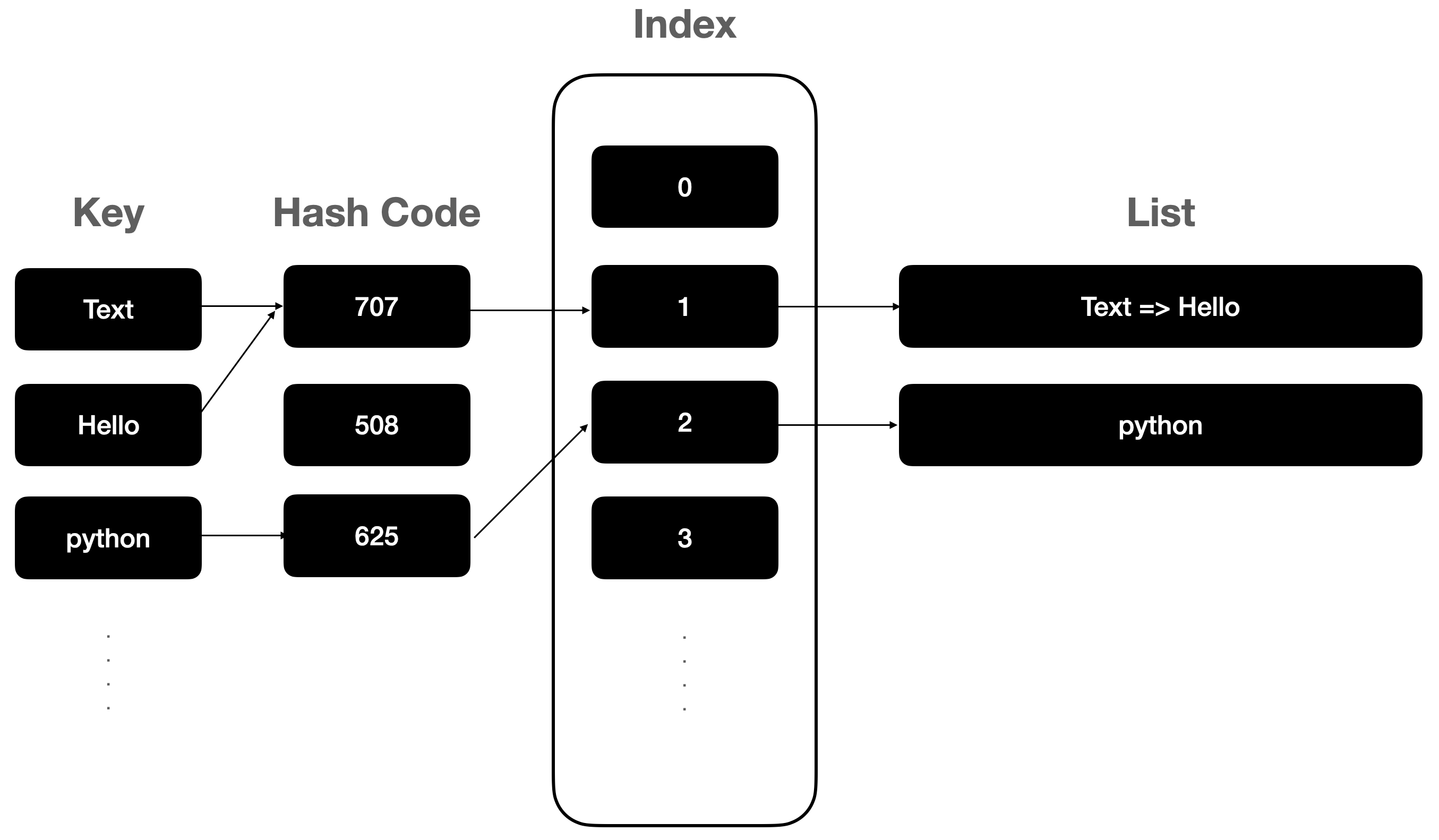
해쉬 테이블(Hash Table)은 해쉬 함수로 만들어진 해쉬 코드(Hash Code)를 담고 있는 테이블(표)이다. 이 테이블은 인덱스를 가리키고 있고 이 인덱스는 해쉬 Code에 맞는 "Key"를 안내한다. 만약 F()라는 해쉬 함수가 존재한다. 이때 "Text"라는 값이 키값이 들어왔다면 "707"과 같이 특정 정수를 내보는 것이다. 이 값은 어떠한 인덱스에 연결이 되어 있고 이 인덱스는 "Text"라는 값을 안내한다. 이때 "Text"라는 값 다음에 나오는 "Hello"가 있는데 이것이 바로 Collision이다.
[ Collision ]
Collision은 "충돌", "부딪힘" 이라는 뜻이다. 즉 오류가 발생했다는 이야기이다. Collision이 발생하는 원인은 두 가지가 있는데 첫 번째로 각각 다른 Input이 들어왔는데 Hash Code가 같을 때 발생한다. 그리고 두 번째로 다른 Hash Code인데 가리키는 Index가 동일할 경우에 발생한다. Collision이 발생되지 않는 게 가장 좋지만 해쉬 알고리즘이 좋지 않으면 많은 Collision이 발생하는 건 당연하다.
위 그림에서 "Text"와 "Hello"가 동일한 공간에 존재하게 되는 이유는 Hash Code가 가리키는 Index가 같은 곳을 가리키기 때문이다. 이것이 프로그램이라면, 보통은 오류가 발생해서 프로그램이 종료된다. 하지만 이렇게 오류가 발생해서 프로그램이 종료되면 안되기 때문에 예외 처리가 필요하다. 그것이 Collision을 방어하는 방법이 된 것이다.
Collision을 방어하는 방법은 Chainning과 Open Address 이렇게 두가지가 있다. Chaining은 위 그림에서 보는 것처럼 Collision이 발생되었을 때 리스트로 구성하여 값을 하나하나 연결하는 것이다. 두 번째 방법은 Open Address로 Collision이 발생하게 되면 특정 알고리즘을 사용하여 주변 공간(메모리)에 저장하는 것이다.
[ Hash Table Python ]
Hash Table을 파이썬으로는 굳이 구현하지 않아도 된다. 바로 딕셔너리 자료구조로 제공하기 때문이다. Dict를 사용한다는 건 Hash Table을 사용하고 있다고 생각해도 된다. 실제 Hash Table을 만들어서 연습해봐도 되지만, 간단하게 구현할 수 있기 때문에 알고리즘 시험에서는 그 이상을 묻지 않는다.
#Dict Declare
hash_table = {'Name': 'kayser', 'Age': 20, 'Class': 'Senior'}
print(hash_table)
print(hash_table['Name'])
#Update
hash_table['Name'] = 'Sam'
print(hash_table['Name'])
#Remove
del hash_table['Name']
print(hash_table)
> {'Name': 'kayser', 'Age': 20, 'Class': 'Senior'}
> kayser
> Sam
> {'Age': 20, 'Class': 'Senior'}'동굴 속 정보' 카테고리의 다른 글
| ELK 설치와 설정, 하나부터 열까지 (0) | 2021.05.08 |
|---|---|
| Binary Tree Traversal, DFS, BFS (0) | 2021.04.25 |
| 점화식 Recusion Tree로 풀기 (0) | 2021.04.21 |
| Binary Search Algorithm (0) | 2021.04.12 |
| Randomized Algorithm (0) | 2021.04.11 |



