[ Big O, 시간복잡도 ]
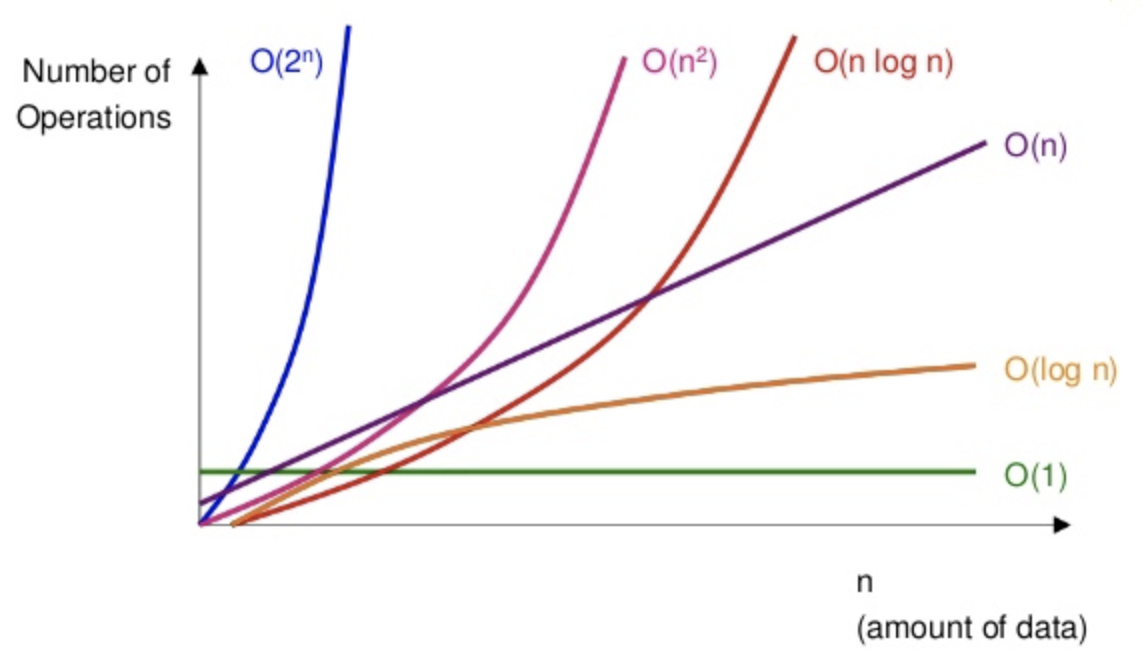
빅오(Big O) 시간복잡도는 위 그림하나도 전부 설명이 가능하다. 빅오는 처리시간이 아니라 시간의 증가율을 나타낸다고 보면 된다. X는 데이터의 갯수, Y는 처리의 갯수이다. 순서를 보면 $O(2^n)$ > $O(n^2)$ > $O(n log n)$ > $O(N)$ > $O(log n)$ > $O(1)$ 이다.
참고로 빅오 표기법에서 상수는 연산에 고정된 값이라서 연산에 크게 작용하지 않는다고 본다. 그래서 상수 10을 빅오랑 곱해도 값은 빅오 그대로 라는 것을 알아야 한다. 예를들어 $10 \times O(1)$ = $O(1)$ 이다.
시간 증가량에 대한 표기법은 점근적 상한(Upper Bound)인 Big-O 외에 점근적 일치(Tight Bound)인 Big-Theta와 점근적 하한(Lower Bound)인 Big-Oega가 있다. 점근적 상한(Big-O)은 Worst Case로 내가 만든 함수 f(n)이 특정 시간 증가율 보다는 낮다라는 의미이다. 점근적 일치는 Best Case와 Worst Case 사이에 내가 만든 F(n)이 있다라는 의미이다. 그리고 점근적 하한(Big-Omega)은 Best Case라서 내가 만든 F(n)이 특정 시간 증가율 보다는 높다라는 의미이다. 이걸 수식으로 확인하면 아래와 같다.
(1) 점근적 상한, Big-Oh($O$) 표기법 :
$f(N) < O(g(n))$
(2) 점근적 일치, Big-theta($\Theta$) 표기법 :
$\Theta(C_1g(n))$ <= $f(N)$ <= $\Theta(C_2g(n))$
(3) 점근적 하한, Big-Omega($\Omega$) 표기법 :
$f(N) >= \Omega(g(n))$
3가지 방법이 있지만, Big-O가 가장 일반적으로 사용된다. 어디에서 이야기하던 전부 빅오로 이야기 하므로 사실 빅오만 알고 있으면 된다고 보면 된다. 이제 오른쪽 $O(1)$부터 왼쪽 $O(2^n)$까지 하나씩 알아보겠다.
[ 시간의 증가율 ]
우선 $O(1)$이다. 입력값의 크기에 상관 없이 일정한 시간으로 처리 시간이 소요되는 작업으로 볼 수 있다. 아래에 있는 코드같은 형태로 시간에 대한 증가 조건이 전혀 발생할 수 있는 형태가 아니라고 보면 된다.
print("Hello World 1\n")
print("Hello World 2\n")
print("Hello World 3\n")
print("Hello World 4\n")
print("Hello World 5\n")
$O(log n)$는 Binary Search 알고리즘을 사용할 때 발생한다. 입력값을 절반씩 반복적으로 나눠고 비교하면서 값을 찾아가는 형식이다.
$O(nlog n)$는 Merge Sort, Quick Sort, Heap Sort 알고리즘을 사용할 때 발생한다. 입력값의 절반이 하나가 남을 때까지 나눈다. 나누어진 개수만큼 비교하는 형식이다. Merge Sort는 반으로 나누는 분할을 사용할 때 $O(log n)$가 되고 합치는 정복을 사용할 때 n개 만큼 비교해야해서 $O(n)$가 된다. 그래서 $O(log n)$ $\times$ $O(n)$ $=$ $O(nlog n)$ 가 된다.
$O(n^2)$는 Bubble Sort, Insertion Sort, Selection Sort 알고리즘을 사용할 때 발생한다. 입력값의 크기에 따라 소요되는 시간이 제곱으로 증가하므로 효율이 좋지 못하다. Bubble Sort는 for문 안에 for문이 있는 구조인 이중For문이다. 이러한 구조가 $O(n^2)$이다.
$O(2^n)$는 대표적으로 피보나치 수열이 있다. 피보나치 수열을 해결하기 위해서는 다이나믹 프로그래밍을 해서 시간을 감소시킬 수 있지만 기본적으로는 무척 가성비 안나오는 형태이다. 재귀함수를 호출할때마다 가지가 두배씩 성장하게되고 반복에 반복을 거치게 되면 그 수는 어마어마하게 뻗어나가게 된다.

[ for 문법 시간 복잡도 ]
(1) for문에서 전체를 반복하는 것이 아닌 일부를 반복하면 $O(logn)$ 이다.
(2) for문에서 전체를 반복하면 $O(n)$이다.
(3) 이중 for문[for(for())]에서 첫번째 for문에서는 전체를 반복하고 두번째 for문에서는 일부만 반복하면 $O(nlogn)$ 이다.
(4) 이중 for문[for(for())]에서 첫번째 for문에서는 전체를 반복하고 두번째 for문에서도 전체를 반복하면 $O(n^2)$ 이다.
'동굴 속 정보' 카테고리의 다른 글
| Randomized Algorithm (0) | 2021.04.11 |
|---|---|
| Greedy Algorithm Python (0) | 2021.04.11 |
| Dynamic Programing Algoritm (0) | 2021.04.10 |
| 최적 알고리즘과, 루프 불변성 (0) | 2021.04.10 |
| 원하는 버전 패키지 yum으로 설치 (0) | 2021.04.06 |



